日々の暮らしと時々の数学

くだらないチラ裏スペース。時々数学のことを書く。

ln(2)を手計算で近似しよう（その１）

すーがく

今回は常用対数ではなく自然対数を手計算で近似してみよう。
次の2種類の近似をする。

計算しやすい評価として

◆評価1◆

  1. {\displaystyle \frac{2}{3}+\frac{2}{81}+\frac{2}{1215}<\ln{2} <\frac{2}{3}+\frac{2}{81}+\frac{2}{1215}+\frac{1}{7\cdot 3^6}}
  2. {\displaystyle \frac{14}{31}+\frac{10}{49}+\frac{6}{161}<\ln{2}<\frac{14}{31}+\frac{10}{49}+\frac{6}{161}+\frac{1}{3\cdot {31}^2}}

を得る。また後々計算できる範囲で項を増やして調節していく。

下4桁のレベル(以下切り捨て)で計算したとすると、前者は
{0.6666+0.0246+0.0016=0.6928<\ln{2}}
であり、後者は{0.4516+0.2040+0.0372=0.6928<\ln{2}}
が得られることになる。
（この評価は前回の記事に用いている。）
より正確な値は次回に回す。

さらに近似の項を増やすと

◆評価2◆

  1. {\displaystyle \frac{2}{3}+\frac{2}{81}+\frac{2}{1215}+\frac{2}{15309}<\ln{2}}で誤差は{\displaystyle \frac{1}{9\cdot 3^8}}未満
  2. {\displaystyle \frac{14}{31}+\frac{10}{49}+\frac{6}{161}+\frac{14}{3\cdot 31^3}<\ln{2}}で誤差{\displaystyle \frac{1}{49^2\cdot 12}}未満

となるが、手計算のレベルで分母が大きい項を精度よく評価するのは
次回として、ぱっと見て分かる程度の補正にすると、

◆評価3◆

  1. {\displaystyle \frac{2}{3}+\frac{2}{81}+\frac{2}{1215}+\frac{1}{10000}<\ln{2}<\frac{2}{3}+\frac{2}{81}+\frac{2}{1215}+\frac{2}{10000}}
  2. {\displaystyle \frac{14}{31}+\frac{10}{49}+\frac{6}{161}+\frac{1.4}{10000}<\ln{2}<\frac{14}{31}+\frac{10}{49}+\frac{6}{161}+\frac{2.2}{10000}}

となる。これは難しく考えることなく得ることができる。

このとき、評価1と評価3について、下4桁で計算した場合から、
下6桁で計算した場合まで、どれほどの精度で見積もれるかを表にした。

f:id:tekitou5353:20151206092030p:plain

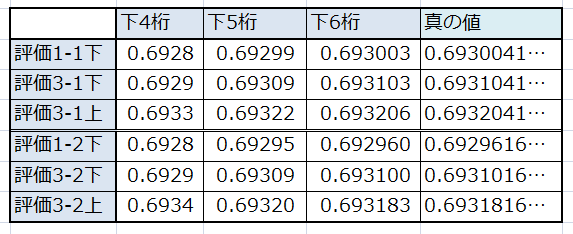
これを見ると、{\ln{2}=0.693\cdots}を確定させるには下5桁、
{\ln{2}=0.6931\cdots}を確定させるには下6桁で計算しておく必要があると分かる。

まず、自然数の自然対数を求めるにあたり、有効な級数を出しておこう。
用いるのは、

◆命題◆
任意の自然数m,nに対し、
{\displaystyle \sum_{i=1}^{n}\frac{2}{(2i-1)(2m+1)^{2i-1}}\leq \log{(m+1)}-\log{m}}
が成立し、その誤差は{\displaystyle \frac{1}{(2n+1)m(2m+1)^{2n}}}未満である。

である。

{-1 < x < 1}であるとき、
{\displaystyle \log{(1-x)}=\sum_{n=1}^{\infty}\frac{x^n}{n}}
という式が成り立つ。

これは、等比級数の和の公式
{\displaystyle \frac{1}{1-x}=1+x+x^2+\cdots}
の項別積分を用いているのだった。

したがって、この等比級数の和を途中で打ち切って積分をする、
あるいはテイラーの定理の積分型の剰余項を利用して
誤差項を評価する。

{\displaystyle \frac{1}{1-x}=1+x+x^2+\cdots+x^{2n-1}+\frac{x^{2n}}{1-x}}
なので，これを0からxまで積分することで、
{\displaystyle -\log{(1-x)}=\sum_{i=1}^{2n}\frac{x^i}{i}+\int_0^x\frac{t^{2n}}{1-t}dx}
とできる。


ここからは{0< x< 1}に限って話をする。
このとき、任意の{0\leq t\leq x}において{\displaystyle \frac{1}{1-t}\leq\frac{1}{1-x}}
が成立するので、
{\displaystyle \sum_{i=1}^{2n}\frac{x^i}{i}\leq -\log{(1-x)}}
{\displaystyle \leq\sum_{i=1}^{2n}\frac{x^i}{i}+\int_0^x\frac{t^{2n}}{1-x}dx=\sum_{i=1}^{2n}\frac{x^i}{i}+\frac{x^{2n+1}}{(1-x)(2n+1)}}
が得られる。

同様に、{0< x< 1}において
{\displaystyle \frac{1}{1+x}=1-x+x^2+\cdots-x^{2n-1}+\frac{x^{2n}}{1+x}}
を0からxまで積分して、
{\displaystyle \log{(1+x)}=\sum_{i=1}^{2n}(-1)^{i-1}\frac{x^i}{i}+\int_0^x\frac{t^{2n}}{1+t}dx}
なので、
{\displaystyle \sum_{i=1}^{2n}(-1)^{i-1}\frac{x^i}{i}\leq \log{(1+x)}}
{\displaystyle \leq\sum_{i=1}^{2n}(-1)^{i-1}\frac{x^i}{i}+\int_0^x{t^{2n}}dx=\sum_{i=1}^{2n}(-1)^{i-1}\frac{x^i}{i}+\frac{x^{2n+1}}{(2n+1)}}

したがって、この2つの評価を足すことで、
{\displaystyle \sum_{i=1}^{n}\frac{2x^{2i-1}}{2i-1}\leq \log{(1+x)}-\log{(1-x)}\leq\sum_{i=1}^{n}\frac{2x^{2i-1}}{2i-1}+\frac{x^{2n+1}(2-x)}{(2n+1)(1-x)}}
が得られる。

ここで、自然数mについて、{\displaystyle x=\frac{1}{2m+1}}を代入することで、
{\displaystyle \sum_{i=1}^{n}\frac{2}{(2i-1)(2m+1)^{2i-1}}\leq \log{(m+1)}-\log{m}}
{\displaystyle \leq\sum_{i=1}^{n}\frac{2}{(2i-1)(2m+1)^{2i-1}}+\frac{(4m+1)}{(2n+1)2m(2m+1)^{2n+1}}}
{\displaystyle <\sum_{i=1}^{n}\frac{2}{(2i-1)(2m+1)^{2i-1}}+\frac{1}{(2n+1)m(2m+1)^{2n}}}
となり、確かに命題の内容が得られた。

さて、これを直接的に用いてそれぞれの評価の1番を得て行こう。
まず、m=1,n=3としたものが、評価1-1、
{\displaystyle \frac{2}{3}+\frac{2}{81}+\frac{2}{1215}<\ln{2} <\frac{2}{3}+\frac{2}{81}+\frac{2}{1215}+\frac{1}{7\cdot 3^6}}
である。

さらに項を増やしてm=1,n=4としたものが、評価2-1、
{\displaystyle \frac{2}{3}+\frac{2}{81}+\frac{2}{1215}+\frac{2}{15309}<\ln{2}}
であって、誤差は{\displaystyle \frac{1}{9\cdot 3^8}}未満となっている。


ここで、手荒いやり方をするが、この評価2-1を計算しやすいように
評価3-1に調節する。
まず、下からの評価については、
{\displaystyle \frac{2}{15309}>\frac{2}{20000}}とすることで得ている。

次に、上からの評価については、まず、誤差が
{\displaystyle \frac{1}{9\cdot 3^8}=\frac{1}{729^2}<\frac{1}{490000}}である。
第4項を計算しやすいように{\displaystyle \frac{2}{15309}<\frac{3}{15000}=\frac{2}{10000}}
で評価すると、これは大体{\displaystyle \frac{1}{15000}}くらい値を大きくしているので、
明らかに{\displaystyle \frac{1}{490000}}を越える。

だから、
{\displaystyle \ln{2}<\frac{2}{3}+\frac{2}{81}+\frac{2}{1215}+\frac{2}{10000}}
と出来るのである。

これらの評価を見ると、4次の項まで展開している。
その必要に迫られているのは、mが小さいためである。
mが大きければ誤差項を見るとべきが2つずつ増えるので、
誤差がすぐ小さくなってくれる。

そこで、mを大きくする方法を考えてみよう。
今回、log2が計算できたのは、m=1とした時にlog1=0となってくれるからであった。
つまり、mを2以上にすると、log2を作れたとしても、他の素因数が出てくる。

この事情を考慮する。
log(m)は、mに現われる素因数のlogの整数係数の線型和になる。
したがって、m+1とmに現われてよい素因数を固定し、
その素因数の数だけmを用意すれば、逆行列を計算することで、
命題の級数の線型和を作ることができる。
（ここら辺は具体的な操作を見た方が早い）

例えば、2と3という素因数が出てくることのみ認めると、
mとしてm=2,8がとれる。これからu=\ln{3}-\ln{2},v=\ln{9}-\ln{8}とし、
また{a=\ln{2},b=\ln{3}}とすると、u,vからa,bを求めるには
\large\left(\begin{array}{cc}1&-1 \\ -3&2 \end{array}\right)
の逆行列を計算すればよい。

このような考えの下、
2,3,5という3つの素因数が出てくることを認めることにする。
すると、（もっと小さく選べるが、大きく選んだほうが有利なので）
m=15,24,80が選べて、c=\ln{5}としておくと、
{p:=\ln{16}-\ln{15}=4a-b-c,}
{q:=\ln{25}-\ln{24}=-3a-b+2c,}
{r:=\ln{81}-\ln{80}=-4a+4b-c}
であるが、

奇跡的に
{A:=\large\left(\begin{array}{ccc}4&-1&-1 \\ -3&-1&2 \\ -4&4&-1 \end{array}\right) \in {\rm GL}_3({\mathbb{Z}})}
と有理整数環の中で話が収まってくれるので、計算量が少なくて済む。
（そうでない場合は、逆行列の成分の大きさに対し、
それを分数で表示したときの桁が大きくなってしまい、計算量が嵩んでしまう。）

よってこれを採用して考えてみよう。
逆行列を計算する（やや負担が大きい）と、
{A^{-1}=\large\left(\begin{array}{ccc}7&5&3 \\ 11&8&5 \\ 16&12&7 \end{array}\right)}
が求まる。
したがって、
{\ln{2}=7p+5q+3r}
である。

これを用いて、m=15,24,80の場合の命題をn=1で打ち切ると、評価1-2の下からの
{\displaystyle \frac{14}{31}+\frac{10}{49}+\frac{6}{161}<\ln{2}}
を得ることができる。
この時の誤差は3種類出てくるが、面倒なので、
最も大きいpの誤差でq,rの誤差も押えておくと、
\displaystyle \frac{7+5+3}{3\cdot 31^2\cdot 15}=\frac{1}{3\cdot 31^2}
と見積もれる。

精度を上げよう。
pの影響がm的にも線型和の係数的にも最も大きいので、
pだけn=2まで項をとると、
{\displaystyle \frac{14}{31}+\frac{10}{49}+\frac{6}{161}+\frac{14}{3\cdot 31^3}<\ln{2}}
を得ることができる。

今度は、qの誤差が一番大きくなったので、これに揃えて誤差評価をしてみよう。
p,q,rから出てくる誤差はそれぞれ\displaystyle \frac{7}{5\cdot 31^4\cdot 15},\frac{5}{3\cdot 49^2\cdot 24},\frac{3}{3\cdot 161^2\cdot 80}である。

このとき、\displaystyle \frac{5\cdot 31^4\cdot 15}{7},161^2\cdot 80はともに
明らかに3\cdot 49^2\cdot 24の2倍よりも大きい。
だから、誤差の和は\displaystyle \frac{5}{3\cdot 49^2\cdot 24}+\frac{1}{3\cdot 49^2\cdot 24}=\frac{2}{49^2\cdot 24}で
評価できる。
これが評価2-2の誤差である。


最後にこれを計算しやすく調整して評価3-2になおそう。
まず、3\cdot 31<100,31^2=961<1000なので、3\cdot 31^3<100000を使えば
下からの評価は簡単に得ることができる。
（log[10]2では散々32^2=1024≒1000を使った。
31の平方は1000を越えないぎりぎりであると知っておくべきである。）

次に、まず誤差項について、49^2>50\cdot 48であり、
（49を減らして48を増やすと左辺が右辺になるから。
和が一定の下では平均に近いほど積は大きい。）
同様の原理で48\cdot 24>50\cdot 22なので、
\displaystyle \frac{2}{49^2\cdot 24}<\frac{2}{50^2\cdot 22}<\frac{2}{50^2\cdot 20}=\frac{0.4}{10000}
が従う。

さらに、{\displaystyle \frac{14}{3\cdot 31^3}}を上から簡単に評価すると、
{\displaystyle \frac{14}{3\cdot 31^3}<\frac{8.1}{3\cdot 30^3}\cdot \frac{14}{8}=\frac{1.75}{10000}}

だから、
{\displaystyle \frac{1.4}{10000}<\frac{14}{3\cdot 31^3}<\frac{1.8}{10000}}

よって、誤差を合わせて
{\displaystyle \ln{2}<\frac{14}{31}+\frac{10}{49}+\frac{6}{161}+\frac{1.8}{10000}+\frac{0.4}{10000}}
{\displaystyle =\frac{14}{31}+\frac{10}{49}+\frac{6}{161}+\frac{2.2}{10000}}
が得られた。

今回の記事は主に解析概論を中心に参照した。

見返してみて、\ln{2}は偶然にもp,q,rの”七五三”だなあと感じた。
3辺の長さが7,5,3の三角形は内角に120度が出てくるからなんともいい組み合わせだ。